Figure 1 (a) Variational circuit to estimate ground state energy of the Heisenberg-spin 1/2 Hamiltonian on a Kagome lattice. (b) Iteration results of (a) using a Constrained Optimization BY Linear Approximation technique (COBYLA). (c) Zero-noise extrapolation result of ibmq_guadalupe with relative error = 0.12 %.
Figure 2 (a)-(c) Structure of Kagome lattice and Qubit layout of ibmq_guadalupe. (d)-(i) Applying HEIS and SWAP gate to initial singlet state to build Hamiltonian Variational Ansatz.
Figure 3 (a) Definition of HEIS gate. (b) Decomposition of HEIS gate to see the number of gates needed for a hardware run. (c) Optimized HEIS gate reducing the CNOT gates counts from 6 to 3.
Contributions: J. Jung developed ran a hardware and simulation experiments, fine-tuned variational ansatz and optimization components, and developed the error mitigation protocols. Jinwoo Yu developed Hamiltonian Variational Ansatz. Junho Lim and Hokyun Lim wrote a supplemental materials.
Variational Quantum Eigensolver Feb. 2023 – Apr. 2023
Preparing the ground state of a Heisenberg spin-1/2 Hamiltonian on a Kagome lattice using the Variational Quantum Eigensolver (VQE)
⌜In IBM open science prize 2022, built Hamiltonian variational ansatz (HVA) based on adiabatic theorem and
trotterization.
Calculated ground state energy of Heisenberg spin-1/2 Hamiltonian (12 qubits) using 16-qubit ibmq_guadalupe system
along with readout error mitigation and zero-noise extrapolation with relative error rate below 0.15 %⌟
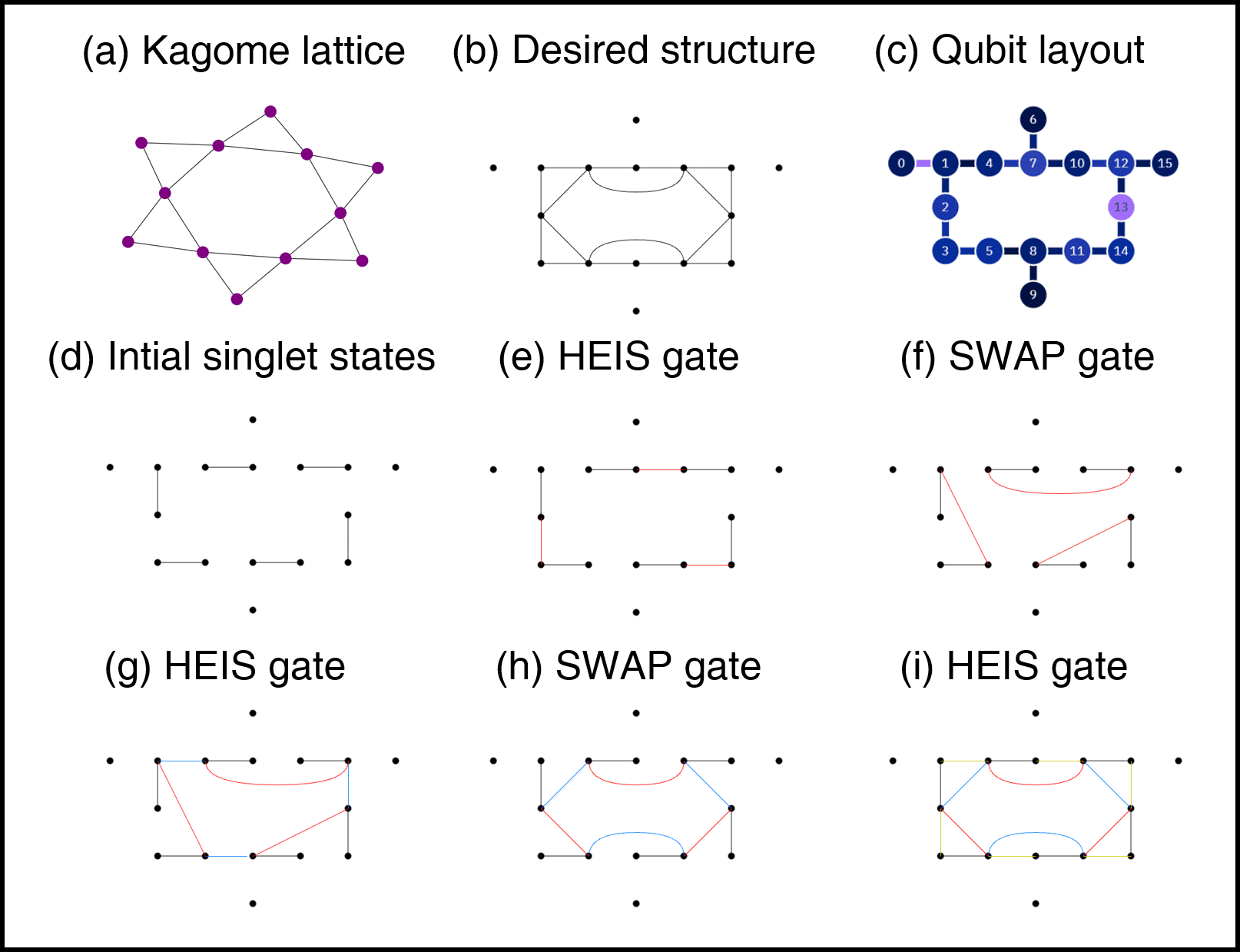
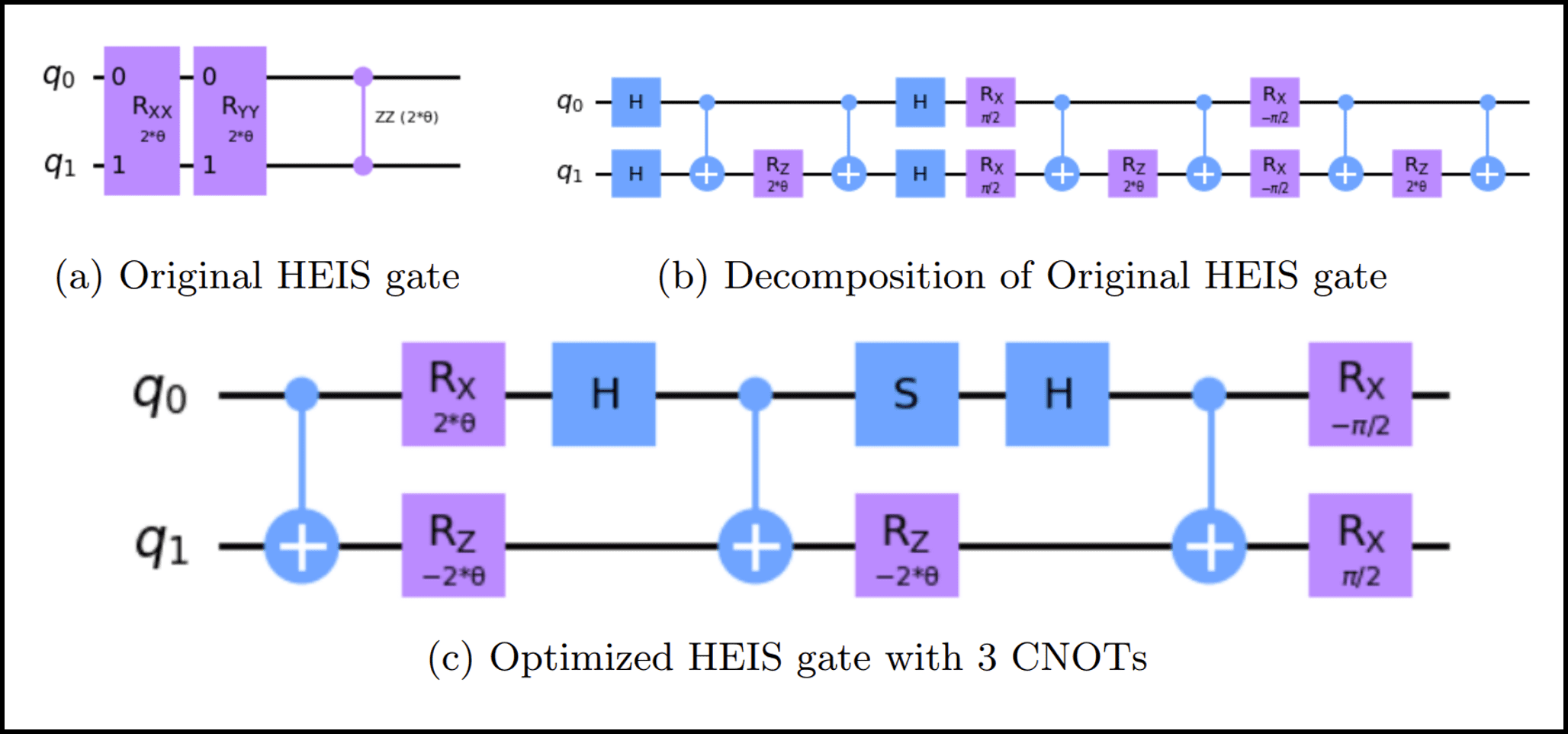
In this project, our team focused on preparing the ground state of a Heisenberg spin-1/2 Hamiltonian on a Kagome lattice using the Variational Quantum Eigensolver (VQE). The Hamiltonian Variational Ansatz (HVA) was employed, leveraging the 16-qubit IBM Quantum Experience device, ibmq guadalupe. A novel approach was used for applying unitary gates on real quantum hardware, supported by various error mitigation techniques, particularly zero-noise extrapolation (ZNE). The optimization process was carried out by carefully designing the ansatz and addressing the challenges related to non-commuting Hamiltonian terms through Trotterization.
We successfully demonstrated the feasibility of applying VQE to complex lattice structures, achieving ground state energy calculations with relative errors within 0.15 % after error mitigation. The study also highlighted the importance of circuit optimization, including reducing the number of CNOT gates and aligning the qubit layout with the hardware's physical constraints to minimize decoherence and other sources of error. Despite technical challenges such as barren plateaus and limitations in the error mitigation process, the results underscored the potential of quantum algorithms for simulating complex quantum systems on near-term quantum hardware.